Những ai từng trải qua kỳ thi đại học và tốt nghiệp cấp ba, trước khi môn toán chuyển sang dạng đề thi trắc nghiệm, hẳn sẽ nhớ rất rõ, và dai dẳng, yêu cầu của bài đầu tiên: khảo sát hàm số. Dầu tất cả các câu sau có là gì chăng nữa, bài đầu tiên vẫn là khảo sát hàm số; và vì được coi là dễ lấy điểm nhất, bất kỳ học sinh nào cũng sẽ phải làm đi làm lại, luyện cho nát dạng bài này.
Năm tôi thi đại học, môn lý và hóa đã đổi sang thi trắc nghiệm, nhưng môn toán vẫn bám theo đề bài truyền thống. Tôi không còn nhớ rõ chi tiết, nhưng bằng vài thao tác gúc đơn giản, tôi tìm ra đề thi môn toán khối A năm đó (khả năng cao) là như sau:
Học sinh cuối cấp ba ngày đó luôn dành rất, rất nhiều thời gian học chỉ để luyện các bài khảo sát hàm số, và làm như một cái máy, vì đã có sẵn template của đề bài, yêu cầu luôn gói gọn trong một vài thao tác: lấy đạo hàm, khảo sát biến thiên, vẽ đồ thị, xác định điểm cực đại và cực tiểu, etc. kèm theo một vài mở rộng không đáng kể khác.
Khi trưởng thành, rất nhiều người trong chúng tôi hay nói đùa, nhưng thật lòng, là không thể nhớ được tại sao hồi xưa mình lại “làm được” những bài mang đầy tính kỹ thuật như thế - thật ra, cứ luyện nhiều thì làm được thôi. Và thứ nữa, là cuối cùng học mòn mỏi những thứ ấy để làm gì; nếu không kể những ai đi theo con đường kỹ sư, thì thi đại học xong, không bao giờ gặp lại và đụng chạm những thứ ấy nữa.
***
Giải quyết được vấn đề “học khảo sát hàm số để làm gì” sẽ là viên gạch đầu tiên để trả lời câu hỏi “học toán để làm gì?, vì một thực tế chúng ta có, như tôi đã nói, học sinh dành rất, rất nhiều thời gian để làm dạng bài này. Đời người là hữu hạn (nếu có thêm thời gian ở cấp 3, tôi sẽ học thêm bóng chuyền), câu nói nửa đùa nửa thật về việc một người 40, 50 tuổi rốt cuộc không cần biết khảo sát hàm số để làm gì, thật ra là một dạng trauma. Ai cũng đã từng đánh vật với “nó”. Để làm gì, rồi nó có ý nghĩa gì trong cuộc đời này?
Câu hỏi nêu trên là cách tóm gọn cho cách nhìn của tôi: rằng cải cách việc học không đơn thuần là làm cho môn học thú vị hơn, vì mỗi một học sinh sẽ luôn tìm cho mình những môn mình thích và những môn mình không thích; mỗi một học sinh sẽ chỉ luôn hứng thú với những gì họ thích, dù sách giáo khoa có dở đến đâu, thầy cô giáo có dạy chán đến đâu chăng nữa. Tức là cải cách chương trình dạy kiểu gì cũng có những môn, những thứ mà anh hay chị học sinh đó không thể buộc cho mình thích được.
Cải cách việc học còn là hướng người học đến một triết lý về “lifelong learning”. Nói hơi nghịch lý, đời người hữu hạn, nhưng học là một việc suốt đời. Một học sinh 15 tuổi sẽ thấy di truyền học Mendel là một thứ rất chán và chẳng để làm gì, nhưng một người trung niên, năm 50 tuổi mới mua được căn nhà và có mảnh vườn tương đối, bắt đầu trồng cây, trồng hoa, trồng rau thơm để ăn phở, họ tìm mua hạt giống, học cách trồng, tưới vào một mùa thích hợp, học cách luân canh để cây to không lấy hết dinh dưỡng của cây nhỏ, etc., thì những thứ ngày xưa học ở môn sinh lại trở nên thú vị.
Chạm vào những thứ thực tiễn, lục lại những thứ mình đã từng học hoặc được nghe mang máng, và có phương tiện để học lại và bồi bổ những thứ ấy, mà không để chúng mất đi vĩnh viễn, mới thực sự là mục đích của sự thay đổi trong cách dạy và học. Để được như thế cần hai thứ: niềm hứng thú và phương tiện. Hứng thú và sự tò mò sẽ đi cùng với một người luôn ở trong tâm thế người học đến hết cuộc đời. Phương tiện là những thứ mà xã hội cung cấp: người dạy, tài liệu mở, lớp học buổi tối cho người lớn về các loại hobby, và các cộng đồng mà người học có thể áp dụng những thứ mình học được, hoặc đơn giản là chia sẻ niềm vui với những người cùng sở thích.
***
Đó là về triết lý. Còn về thực tiễn, ta sẽ thử đề ra một cách để giải quyết viên gạch đầu tiên, như đã nói: bài khảo sát hàm số, học để làm gì?
Tôi sẽ kể một chút về một buổi sáng không mấy đặc biệt của tôi ở chỗ làm. Một sáng thứ Ba, tôi sẽ đến trường từ sớm, bắt đầu một tuần làm việc mới (vì thứ Hai thường dành để giải quyết giấy tờ và tất tật những việc khác). Tôi xuống căn tin trường, mua bánh ăn sáng và một ly cà phê, cầm theo tờ báo mà người ta giao từ thứ Năm tuần trước đó nhưng chưa có thời gian đọc. Tôi đọc bài phỏng vấn Hannah Ritchie, một nhà khoa học về môi trường người Scotland. Tôi nghe nói đến cô này vì cổ viết sách cho độc giả đại chúng để người ta bớt panic về biến đổi khí hậu. Tờ Die Zeit tôi hay đọc là tờ báo cánh tả, trụ sở ở Hamburg.
Một cuộc sống “tốt” theo quan điểm của Ritchie là ở đó người ta có thể tiếp cận các dịch vụ y tế và giáo dục cần thiết, tiếp cận nước sạch, đồ ăn, năng lượng, điện đóm, và được bầu cử tự do. Mảng của cổ là nghiên cứu dữ liệu về môi trường, tức là thông qua dữ liệu lịch sử, làm sao chúng ta có thể miêu tả thế giới thực và hiện tại của mình một cách chính xác hơn.
Trong bài báo có đoạn (đánh dấu"):
Ritchie: Tin tốt tiếp theo sẽ là chúng ta sắp đạt đỉnh về lượng phát thải CO₂ toàn cầu. Các chuyên gia vẫn chưa thống nhất liệu điều này sẽ xảy ra trong năm nay hay năm tới. Nhưng nó rất có khả năng sẽ xảy ra sớm. Hiện tại, lượng phát thải vẫn đang tăng, nhưng tốc độ tăng đã chậm lại đáng kể. Câu chuyện này gắn liền với sự phát triển nhanh chóng của năng lượng xanh, một yếu tố đóng góp rất lớn. Quá trình này đang diễn ra nhanh hơn nhiều so với dự kiến. Nếu Trung Quốc đạt đỉnh, điều đó sẽ đánh dấu bước ngoặt cho Trái Đất.
Thế giới sắp đạt đỉnh về CO2 emission, và điều này có khả năng sẽ xảy ra sớm, vào năm nay hay năm tới. “Điều này” cụ thể là điều gì? Tôi có thể hình dung được cách hiểu của Ritchie, nhưng đồng thời muốn phác thảo một biểu đồ. Vì thế tôi nhờ bạn mình vẽ một hàm đại khái biểu thị CO2 emission theo ý của bài báo:
Ở hình trên, ChatGPT thể hiện lượng phát thải CO2 bằng hàm E(t) = -at^2 + bt + c có dạng parabol. Ban đầu, lượng phát thải tăng lên, sau đó chậm lại, đạt đỉnh và hạ xuống. Đường kẻ chấm bên dưới là đạo hàm E'(t) = -2at + b thể hiện tốc độ thay đổi của lượng khí thải. Khi đạo hàm bằng 0 thì lượng phát thải đạt giá trị cực đại và ngừng tăng. Sau đó, đạo hàm bé hơn 0 thể hiện lượng phát thải đang giảm. (Lưu ý là thằng ChatGPT hơi man mát nên không phải mọi chi tiết nó thể hiện đều chuẩn xác.)
Đây là một hàm lý tưởng nên khá smooth. Đạo hàm E’(t) cho thấy tốc độ tăng trưởng của lượng phát thải đang chậm lại theo thời gian. Khi đạo hàm bằng không, điều này tương ứng với đỉnh phát thải CO₂, phù hợp với quan điểm trong bài báo rằng lượng phát thải sẽ sớm ngừng tăng và có thể bắt đầu giảm xuống. Như vậy, ứng dụng của đạo hàm (bậc một) là cho ta thấy khi nào lượng phát thải CO2 đạt cực đại - điều này có thể xảy ra vào một năm 203x nào đó.
Nhưng dĩ nhiên, thực tế diễn ra không phải lúc nào cũng suôn sẻ như vậy. (Một hàm được gọi là smooth, về mặt kỹ thuật, có những điều kiện rất chặt chẽ.) Chúng ta sẽ cần đến những hàm phức tạp hơn và, đôi khi, cần khảo sát những đạo hàm bậc cao để có cái nhìn gần chính xác hơn.
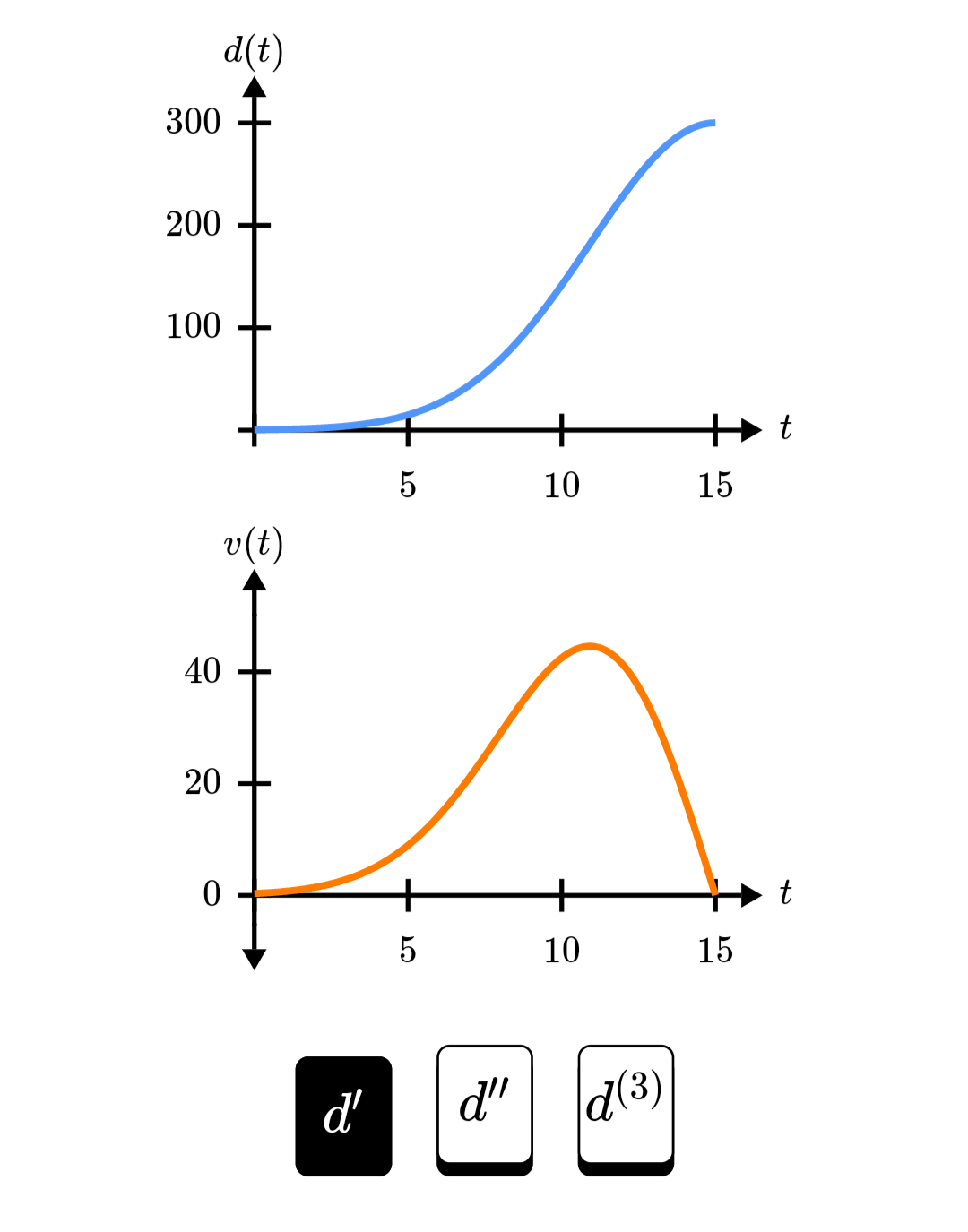
Vì bài báo chỉ nêu là lượng phát thải sắp đạt đỉnh (“lượng phát thải vẫn đang tăng, nhưng tốc độ tăng đã chậm lại đáng kể”), nên anh bạn ChatGPT giả định là sau đó lượng khí thải tuột dốc là hơi “bốc”. Chúng ta có thể ước lượng lại bằng hàm d(t) màu xanh như hình trên: t biểu thị thời gian, d(t) tăng rất nhanh trong quãng t từ 5 đến 10, nhưng sau đó chững lại. Khi xem xét đạo hàm bậc một d’(t), ở đường màu cam hình dưới, ta thấy đường màu xanh đạt độ dốc cực đại là khi t = 10, đồng nghĩa lúc này đạo hàm d’ đạt cực đại. Theo sát câu nói của Hannah Ritchie thì chúng ta đã vượt qua điểm này (độ dốc lớn nhất), đạo hàm d’(t) đã vượt qua điểm cực đại và giờ đang giảm xuống.
Ta xét tiếp đạo hàm bậc hai d’’(t):
Đạo hàm bậc hai thể hiện độ dốc của đạo hàm bậc một, tức là nếu d’ thể hiện tốc độ tăng của lượng phát thải CO2 thì d’’ (hai phẩy) thể hiện gia tốc. Gia tốc cực đại đạt được ở điểm giữa t=5 và t=10, sau đó về “mo” và đạt gia tốc âm từ khoảng t = 11, tức là lúc này tốc độ tăng bắt đầu giảm mạnh.
Lại xét tiếp đạo hàm bậc ba, tức d‘‘‘ (ba phẩy):
Tại điểm d ba phẩy bằng 0, thể hiện lúc d hai phẩy đổi dấu từ dương sang âm. Sau đó d ba phẩy đạt cực tiểu. Vậy điều gì diễn ra ở hàm chính d(t) thời điểm đó? Nói nôm na, d ba phẩy đạt cực tiểu thể hiện một cú hãm mạnh, khiến độ dốc của đường màu xanh thay đổi mạnh và quay sang hướng nằm ngang (sau đó có hạ xuống không thì ta chưa biết, ta chỉ giả định đến điểm này thôi.)
Như vậy với ứng dụng của đạo hàm bậc một tới bậc ba, ta có thể có sự hình dung rõ hơn, gần chính xác hơn về việc lượng phát thải CO2 sắp không còn tăng nữa, và chững lại, nghĩa là như thế nào. Sau đó, ta chưa biết, ta chỉ biết tới đoạn nó đang dần chững lại.
Tới đây, tôi có thể tiết lộ ba hình đồ thị trên (mà tôi tạm lấy đường màu xanh thể hiện lượng phát thải CO2) thể hiện điều gì. Đó là hình tôi chụp trong app Brilliant, một app dùng để ôn toán. Đây là tôi đang học lại môn Calculus. Đường màu xanh f(t) thể hiện quãng đường của một chiếc xe hơi đang chạy từ giây số 0 đến giây thứ 15. Đạo hàm d’ thể hiện vận tốc, max của d’ chỉ vận tốc cực đại. Sau đó người lái thắng xe lại.
Đạo hàm bậc hai d’’ thể hiện gia tốc. Gia tốc tăng tới cực đại khi người lái đạp ga, gia tốc giảm khi người lái đạp thắng (một cách ước chừng, vì thật ra do nhiều yếu tố cơ học cũng khó biết rõ thời điểm nào thì đạp thắng).
Đạo hàm bậc ba d’’’ thể hiện độ dốc của gia tốc. d’’’ chạy qua điểm cực tiểu là khi trong ngành cơ khí ô tô người ta gọi một cú “jerk”. Đoạn t=10 đến 15 là khả năng cao có một cú jerk xảy ra.
Năm vừa rồi tôi thi rớt lái xe, nên tôi biết rõ xe bị jerk này là như thế nào: tức là khi ta đạp phanh hơi mạnh quá, xe bị hãm lại đột ngột, nhanh hơn mức mà máy móc của nó cho phép, xe sẽ bị giật cục, ta gọi là “jerk”. Người kỹ sư cơ khí khi thiết kế hệ thống phanh sẽ phải nghiên cứu rất kỹ đường d’’’ này. Tương tự, người học lái xe phải lái làm sao mà đạp phanh đừng để bị giật cục.
Việc giật cục không đơn giản là do lái non tay, mà còn hay xảy ra khi ta bắt đầu học cách thắng gọi là “degressive break”, tức là đạp phanh vào đúng điểm để gây đủ áp lực phanh lên bánh trước, sau đó nhả phanh ra từ từ - làm cách này giúp tránh hao mòn phanh và tiết kiệm nhiên liệu. Đạp phanh sớm thời điểm hay mạnh hơn mức cần thiết đều có thể gây ra giật cục.
Dĩ nhiên, tôi sẽ chẳng bao giờ thực sự tìm hiểu những điều này, nếu như một ngày nào đó, tôi không thi rớt thực hành lái xe.